[알고리즘 정렬] 자바(JAVA)로 알아보는 퀵 정렬(Quick Sort)

퀵 정렬(Quick Sort)

퀵정렬을 하기 위해 가장 먼저 해야 하는 것: 기준점(pivot) 잡기

기준점(pivot) 값을 정할 때에는 아무 값이나 정해도 되지만 중간 값으로 잡는 게 가장 좋다.
- 피벗 선택 방식: 첫 번째, 중간, 마지막, 랜덤 등등 (선택 방식에 따라 속도가 달라짐) 다양함
하지만 우리는 배열을 검색해보고 나서 중간값이 어딘지를 정할 수 없기 때문에 그냥 물리적으로 중간에 있는 값을 선택(배열의 길이가 n라고 치면 n/2의 값을 기준점으로 잡음)

아무 곳을 기준점으로 잡고 기준점을 기준으로 기준점보다 작거나 같으면 smaller, 기준점보다 크거나 같으면 bigger(기준점을 smaller에 포함시켜도 되고 bigger에 포함시켜도 된다)로 나눈다.
퀵 정렬의 전제는 작은 쪽(smaller)과 큰 쪽(bigger)을 나누고 이 둘을 각각 정렬하면 결국 전체적으로 정렬이 완성된다는 것이다.

위에서 나눈 두 부분 중 smaller에서 먼저 아무 곳이나 기준점을 잡는다(아무 곳이나 기준점을 잡는 것이기 때문에 이 기준점이 얼마나 치우친 값인지 알 수는 없음)
파티션들을 쪼개고 쪼개다 보면 결국 파티션 안의 배열이 2개만 남음(초록색 bigger부분)
- -> 그 두 개 중에서 작은 것(smaller)과 큰 것(bigger)을 정렬(결국 낱개가 될 때까지 smaller과 bigger를 나눈다)
==> 재귀함수를 반환할 때에는 정렬된 상태로 반환하게 됨

퀵 정렬 시간 복잡도

O(n log n): 평균적으로 이 정도고 최악의 경우 O(n²)까지 나올 수 있다. 하지만 대개 O(n log n)이라고 함
- 이유: 배열을 나누는 횟수가 n번임 -> 배열을 낱개가 될 때까지 나누기 때문에
  - 처음 나누고 나면(파란색 부분) 두 번째 나눌 때에는 n을 둘로 나눈 결과(초록색 부분)를 가지고 나누게 됨 -> 검색해야 하는 데이터가 절반으로 줄어듦(log n의 시간 복잡도)
  - ==> n만큼 파티션을 나누는데 나눌 때마다 데이터가 절반씩 줄어드니까 n * log n = O(n log n)

시간 복잡도 최악의 경우 O(n²)의 예시

[ 첫 번째 기준점 ]

1. 물리적으로 가운데에 있는 0을 기준점(pivot)으로 잡는다

2. 우연히 기준점이 제일 작은 값임

정렬 결과

[ 두 번째 기준점 ]

1. bigger 파티션에서 물리적으로 가운데에 있는 1을 기준점(pivot)으로 잡는다

2. 1도 우연히 기준점이 제일 작은 값임

정렬 결과

이렇게 계속해서 기준점이 가장 작거나 혹은 가장 클 때의 시간 복잡도는 O(n^2)이 된다

시간 복잡도 O(n log n)의 예시

start point: pivot값보다 작은 값들은 무시하면서 뒤로 감
end point: pivot값보다 큰 값들은 무시하면서 앞으로 감

=> start point와 end point가 뒤바뀌게 되면(한 번의 루프가 끝나면) pivot값보다 작은 값들과 큰 값들로 나뉘게 됨

첫 번째 루프

첫 번째 정렬

start point(3)가 pivot값(5)보다 작으므로 건너 뜀

두 번째 정렬

start point(9)가 pivot값(5)보다 크므로 기다림
end point(2)가 pivot값(5)보다 작으므로 start point와 end point를 swap함
start point와 end point를 한 칸씩 이동

swap 결과

세 번째 정렬

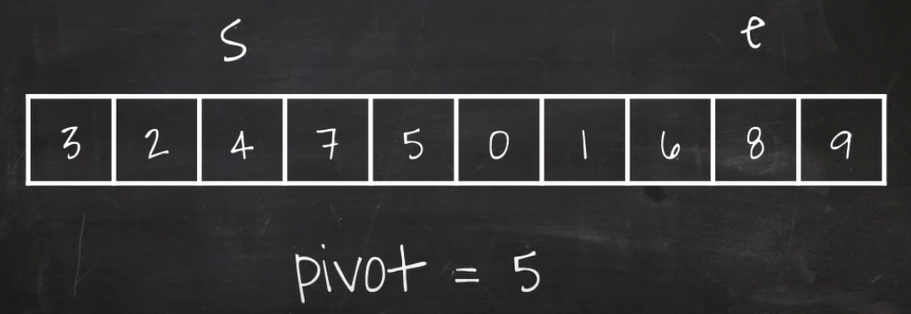
start point(4)가 pivot값(5)보다 작으므로 건너 뜀

네 번째 정렬

start point(7)가 pivot값(5)보다 크므로 기다림
end point(8)가 pivot값(5)보다 크므로 건너 뜀

end point(6)가 pivot값(5)보다 크므로 건너 뜀

end point(1)가 pivot값(5)보다 작으므로 start point와 end point를 swap함
start point와 end point를 한 칸씩 이동

swap 결과

다섯 번째 정렬

start point(5)가 pivot값(5)와 작지 않으므로(같으므로) 멈춤
end point(0)가 pivot값(5)보다 작으므로 start point와 end point를 swap함
start point와 end point를 한 칸씩 이동

swap 결과

start point와 end point가 서로의 조건을 벗어나버림(뒤바뀜) -> 조건문의 범위를 벗어났으므로 루프 종료
현재 start point가 가리키고 있는 것: 두 번째 배열방의 첫번째 인덱스(5) ==> 그 방 번호를 함수의 결과로 반환

첫 번째 루프에서 얻었던 두 번째 배열방의 첫번째 인덱스(5) -> bigger방의 첫 번째 인덱스 혹은 smaller 방의 마지막 인덱스로 넣어줌(둘 중 어느 것으로 해도 상관 없음!)
양쪽 파티션의 값이 각각 2개 이상인 경우에는 정렬을 해야 함

퀵 정렬을 트리로 나타낸다면?

만약 나눈 파티션이 쏠려있다면?

하나만 남은 파티션은 더 이상 재귀 호출을 하지 않는다

퀵 정렬 자바로 구현해보기

public class Test {
    private static void quickSort(int[] arr){
        quickSort(arr, 0, arr.length - 1); // 시작 위치와 끝나는 위치를 받아서 재귀 함수를 호출해줌
    }

    private static void quickSort(int[] arr, int start, int end){
        int part2 = partition(arr, start, end); // 배열의 시작과 끝 영역 안에서 파티션을 나눔 -> 나눈 파티션의 오른쪽 방 첫 번째 값(인덱스)을 받아옴
        /*
            오른쪽 파티션이 시작점 바로 다음에서 시작(== 오른쪽 파티션이 시작점에서 한 개 차이) -> 왼쪽 파티션의 데이터가 하나(쏠려있는 현상인 경우) ==> 더 이상 정렬할 필요가 없음
            [3, 5, 4, 2, 1]인 경우
            [    3    |   5, 4, 2, 1]
              smaller |     bigger

            => smaller 파티션의 값이 하나이므로 정렬할 필요가 없음.
        */

        if(start < part2 - 1){ // 오른쪽 파티션이 시작점에서 한 개 이상 차이가 날 때만(쏠려있지 않은 경우에만) 함수를 재귀적으로 호출하게 함
            quickSort(arr, start, part2 - 1); // 시작과 끝 점을 조정해서 재귀 호출. part2가 오른쪽 방 첫 번째 값이니까 (part2 - 1)은 왼쪽 방의 마지막 인덱스 값
        }

        if(part2 < end){ // 오른쪽 배열방의 값이 2개 이상일 때만 호출 ==> 오른쪽 파티션의 시작점이 배열의 마지막 값보다 작은 경우에만 재귀 함수 호출
            // 오른쪽 파티션의 시작점 == 배열의 마지막 값 -> 오른쪽 배열의 값이 하나 있고 그 값이 시작점 값임. 따라서 이런 경우에는 정렬할 필요가 없으니까 이러한 경우를 제외할 때만 재귀함수를 호출해야 한다.
            quickSort(arr, part2, end);
        }
    }

    private static int partition(int[] arr, int start, int end){
        int pivot = arr[(start + end) / 2]; // 기준점: 배열의 처음과 끝 값의 중간지점
        while(start <= end){ // 시작점이 끝점보다 작거나 같을 때만 시작점을 앞으로 한칸씩 옮김
            while(arr[start] < pivot) start++; // 배열방의 값이 피벗값보다 작은 경우에(정상적인 경우) 시작점을 한 칸씩 옮김(통과)
            while(arr[end] > pivot) end--; // 배열방의 값이 피벗 값보다 클 경우에만(정상적인 경우) 끝점을 한 칸씩 옮김(통과)
            if(start <= end){ // 시작점이 끝점을 지나쳤는지 다시 한번 확인해준 후에
                swap(arr, start, end); // 두 점을 바꿔줌(시작점이 피벗 값보다 큰 경우 + 끝점이 피벗 값보다 작은 경우)
                start++; // 시작점을 한칸씩 옮김
                end--; // 끝점을 한칸씩 옮김
            }
        }

        return start; // 새로 나눌 오른쪽 파티션의 첫 번째 배열방 인덱스를 반환
    }

    private static void swap(int[] arr, int start, int end){
        int temp = arr[start];
        arr[start] = arr[end];
        arr[end] = temp;
    }

    private static void printArray(int[] arr){ // 배열 확인용 출력 메소드
        for(int data : arr){
            System.out.print(data + " ,");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        int[] arr = {3, 9, 4, 7, 5, 0, 1, 6, 8, 2};
        printArray(arr);
        quickSort(arr);
        printArray(arr);
    }
}

코드만 정리

public class Test {
    private static void quickSort(int[] arr){
        quickSort(arr, 0, arr.length - 1);
    }

    private static void quickSort(int[] arr, int start, int end){
        int part2 = partition(arr, start, end);

        if(start < part2 - 1){
            quickSort(arr, start, part2 - 1);
        }

        if(part2 < end){
            quickSort(arr, part2, end);
        }
    }

    private static int partition(int[] arr, int start, int end){
        int pivot = arr[(start + end) / 2];
        while(start <= end){
            while(arr[start] < pivot) start++;
            while(arr[end] > pivot) end--;
            if(start <= end){
                swap(arr, start, end);
                start++;
                end--;
            }
        }

        return start;
    }

    private static void swap(int[] arr, int start, int end){
        int temp = arr[start];
        arr[start] = arr[end];
        arr[end] = temp;
    }

    private static void printArray(int[] arr){
        for(int data : arr){
            System.out.print(data + " ,");
        }
        System.out.println();
    }

    public static void main(String[] args) {
        int[] arr = {3, 9, 4, 7, 5, 0, 1, 6, 8, 2};
        printArray(arr);
        quickSort(arr);
        printArray(arr);
    }
}

출력 결과

출처

https://www.youtube.com/watch?v=7BDzle2n47c&t=504s

https://github.com/gyoogle/tech-interview-for-developer/blob/master/Algorithm/QuickSort.md

저작자표시 비영리 변경금지

'CS > 알고리즘' 카테고리의 다른 글

[알고리즘 정렬] 자바(JAVA)로 알아보는 버블 정렬(거품 정렬 Bubble Sort) (0)	2022.03.25
[이코테 2021 강의] 1. 알고리즘 성능평가 (자바 코드 예시) (0)	2022.03.19

turtleDeveloper

[알고리즘 정렬] 자바(JAVA)로 알아보는 퀵 정렬(Quick Sort)

퀵 정렬(Quick Sort)

퀵 정렬 시간 복잡도

시간 복잡도 최악의 경우 O(n²)의 예시

시간 복잡도 O(n log n)의 예시

첫 번째 루프

첫 번째 정렬

두 번째 정렬

세 번째 정렬

네 번째 정렬

다섯 번째 정렬

만약 나눈 파티션이 쏠려있다면?

퀵 정렬 자바로 구현해보기

코드만 정리

출력 결과

'CS > 알고리즘' 카테고리의 다른 글

댓글

티스토리툴바

[알고리즘 정렬] 자바(JAVA)로 알아보는 퀵 정렬(Quick Sort)

퀵 정렬(Quick Sort)

퀵 정렬 시간 복잡도

시간 복잡도 최악의 경우 O(n2)의 예시

시간 복잡도 O(n log n)의 예시

첫 번째 루프

첫 번째 정렬

두 번째 정렬

세 번째 정렬

네 번째 정렬

다섯 번째 정렬

만약 나눈 파티션이 쏠려있다면?

퀵 정렬 자바로 구현해보기

코드만 정리

출력 결과

'CS > 알고리즘' 카테고리의 다른 글

관련글

댓글

티스토리툴바

시간 복잡도 최악의 경우 O(n²)의 예시