https://www.acmicpc.net/problem/1260
1260번: DFS와 BFS
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사
www.acmicpc.net

문제
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.
입력
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.
출력
첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.
예제 입력 1
4 5 1
1 2
1 3
1 4
2 4
3 4
예제 출력 1
1 2 4 3
1 2 3 4
예제 입력 2
5 5 3
5 4
5 2
1 2
3 4
3 1
예제 출력 2
3 1 2 5 4
3 1 4 2 5
예제 입력 3
1000 1 1000
999 1000
예제 출력 3
1000 999
1000 999
package String;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.LinkedList;
import java.util.Queue;
public class Main {
static int[][] arr;
static boolean[] visited;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] str = br.readLine().split(" ");
int N = Integer.parseInt(str[0]); // 정점의 개수
int M = Integer.parseInt(str[1]); // 간선의 개수
int V = Integer.parseInt(str[2]); // 탐색을 시작할 정점의 번호
arr = new int[N+1][N+1];
// 정점 번호는 1번부터 N번까지이므로 편의상 배열의 크기를 +1해준다.
/*
arr배열의 의미: 정점들이 만나는지 표시를 해주기 위해
arr [N+1] [N+1]
해당 정점 그 정점과 만나는 다른 정점
*/
for(int i = 0; i < M; i++) {
String[] str2 = br.readLine().split(" ");
int a = Integer.parseInt(str2[0]);
int b = Integer.parseInt(str2[1]);
arr[a][b] = 1;
arr[b][a] = 1;
// 입력으로 주어지는 간선은 양방향이므로 둘 다 체크해준다.
}
visited = new boolean[N + 1]; // 방문 여부
dfs(V);
System.out.println();
visited = new boolean[N + 1]; // 여기서 다시 선언을 해주지 않으면 위에 dfs(V)함수에서 사용한 visited를 bfs(V)에서도 사용하게 되므로 초기화 시켜준다.
bfs(V);
}
// dfs -> 재귀 방식을 사용함
static void dfs(int V) {
visited[V] = true; // V: 탐색을 시작할 정점의 번호 -> 해당 번호는 이미 방문한 정점이므로 방문했다는 표식을 남겨줌
System.out.print(V + " ");
if(V > arr.length - 1) {
/*
arr.length는 정점의 갯수에서 +1 한 수이므로 'arr.length - 1 = 정점의 총 개수'
V(탐색을 시작할 정점 번호)가 정점의 총 갯수보다 클 수 없다!!
*/
return;
}
for(int node = 1; node < arr.length; node++) { // j: 정점 번호 -> 정점의 1 ~ 끝 번호까지 반복문을 돌림
// arr[V][node] == 1: 연결된 두 정점이다 / visited[j] == false: 아직 방문하지 않았다
if(arr[V][node] == 1 && visited[node] == false) {
dfs(node); // -> 다시 dfs(j) 함수를 호출해줌(재귀함수) -> 호출하면 이제 방문했다는 표식을 남길 수 있음
}
}
}
// bfs -> 큐(queue) 방식을 사용함
static void bfs(int V) {
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(V); // 큐에 해당 정점 번호를 넣어줌
visited[V] = true; // 방문했다는 표식을 남겨줌
System.out.print(V + " ");
while(!queue.isEmpty()) { // 큐가 비어있지 않으면
int temp = queue.poll(); // 큐에 담겨있는 번호 중 가장 앞에 담겨져있는 번호
for(int node = 1; node < arr.length; node++) {
if(arr[temp][node] == 1 && visited[node] == false) { // 해당 노드와 연결된 다른 노드가 있고 그 다른 노드를 아직 방문하지 않았다면
queue.add(node); // 다른 노드를 queue에 넣고
visited[node] = true; // 방문했다는 표식을 남겨줌
System.out.print(node + " ");
}
}
}
}
}
풀이 설명
예제 1을 기준으로 설명
예제 입력 1
4 5 1
1 2
1 3
1 4
2 4
3 4

- arr 배열 선언: [ [ , , , , ], [ , , , , ], [ , , , , ], [ , , , , ], [ , , , , ] ]
- 1번과 2번 노드 연결 = 2번과 1번 노드 연결 ==> [1, 2]([1][2]), [2, 1]([2][1])
- 1번과 3번 노드 연결 = 3번과 1번 노드 연결 ==> [1, 3]([1][3]), [3, 1]([3][1])
- 1번과 4번 노드 연결 = 4번과 1번 노드 연결 ==> [1, 4]([1][4]), [4, 1]([4][1])
- 2번과 4번 노드 연결 = 4번과 2번 노드 연결 ==> [2, 4]([2][4]), [4, 2]([4][2])
- 3번과 4번 노드 연결 = 4번과 3번 노드 연결 ==> [3, 4]([3][4]), [4, 3]([4][3])
- 간선들을 arr 배열에 입력한 결과: [ [ , , , , ], [ , , 1, 1, 1], [ , 1, , , 1], [ , 1, , , 1], [ , 1, 1, 1, ] ]
- visited 배열 선언: 해당 노드(정점)의 방문 여부를 표시하기 위한 배열
dfs & bfs 탐색 차이
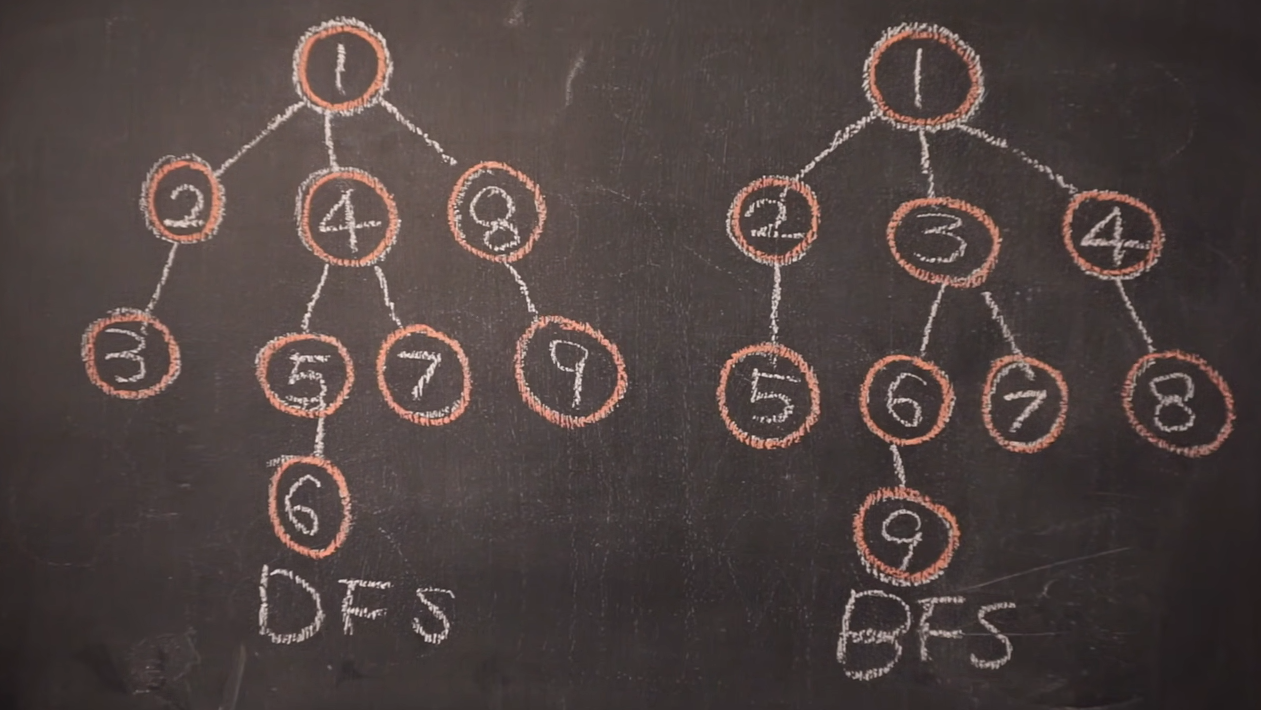
dfs
스택이나 재귀 방식을 사용함(여기서는 재귀를 사용함)
static void dfs(int V) {
visited[V] = true; // V: 탐색을 시작할 정점의 번호 -> 해당 번호는 이미 방문한 정점이므로 방문했다는 표식을 남겨줌
System.out.print(V + " ");
if(V > arr.length - 1) {
/*
arr.length는 정점의 갯수에서 +1 한 수이므로 'arr.length - 1 = 정점의 총 개수'
V(탐색을 시작할 정점 번호)가 정점의 총 갯수보다 클 수 없다!!
*/
return;
}
for(int node = 1; node < arr.length; node++) { // j: 정점 번호 -> 정점의 1 ~ 끝 번호까지 반복문을 돌림
// arr[V][node] == 1: 연결된 두 정점이다 / visited[j] == false: 아직 방문하지 않았다
if(arr[V][node] == 1 && visited[node] == false) {
dfs(node); // -> 다시 dfs(j) 함수를 호출해줌(재귀함수) -> 호출하면 이제 방문했다는 표식을 남길 수 있음
}
}
}
처음 V는 1(예제 1에서 V = 1임)
- visited = [ , O, , , ]
- arr[1][2] == 1 && visited[2] == false -> dfs(2)
V = 2
- visited = [ , O, O, , ]
- arr[2][4] == 1 && visited[4] == false -> dfs(4)
V = 4
- visited = [ , O, O, , O]
- arr[4][3] == 1 && visited[3] == false -> dfs(3)
V = 3
- visited = [ , O, O, O, O]
==> 1 2 4 3 순으로 노드를 지나감
bfs
큐(queue) 방식을 사용함
static void bfs(int V) {
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(V); // 큐에 해당 정점 번호를 넣어줌
visited[V] = true; // 방문했다는 표식을 남겨줌
System.out.print(V + " ");
while(!queue.isEmpty()) { // 큐가 비어있지 않으면
int temp = queue.poll(); // 큐에 담겨있는 번호 중 가장 앞에 담겨져있는 번호
for(int node = 1; node < arr.length; node++) {
if(arr[temp][node] == 1 && visited[node] == false) { // 해당 노드와 연결된 다른 노드가 있고 그 다른 노드를 아직 방문하지 않았다면
queue.add(node); // 다른 노드를 queue에 넣고
visited[node] = true; // 방문했다는 표식을 남겨줌
System.out.print(node + " ");
}
}
}
}
queue 선언
queue에 V(= 1)을 추가
| 1 |
visited = [ , O, , , ]
만약 queue가 비어있지 않다면 반복문 돌리기
int temp -> queue에 담긴 번호 중 가장 앞에 담긴 번호 == 1
if문에 걸리게 되는 node들은 2, 3, 4가 해당됨
1. arr[1][2] == 1 && visited[2] == false
- queue.add(2)
| 2 |
- visited = [ , O, O, , ]
2. arr[1][3] == 1 && visited[3] == false
- queue.add(3)
| 2 | 3 |
- visited = [ , O, O, O, ]
3. arr[1][4] == 1 && visited[4] == false
- queue.add(4)
| 2 | 3 | 4 |
- visited = [ , O, O, O, O]
==> 1 2 3 4 순으로 노드를 지나감
이후에 queue에 담긴 노드 순서대로 반복문을 돌려서 노드들의 자식노드를 차례대로 탐색하고 또 그들의 자식노드들을 차례대로 탐색하면 된다.
이미지 출처
https://www.youtube.com/watch?v=_hxFgg7TLZQ&t=11s
'Coding Test > 백준' 카테고리의 다른 글
| [백준 자바 JAVA] 11047번 동전 0 (0) | 2022.03.26 |
|---|---|
| [백준 자바 JAVA] 1003번 피보나치 함수 (0) | 2022.03.26 |
| [백준 자바 JAVA] 1193번 분수찾기 (0) | 2022.03.20 |
| [백준 자바 JAVA] 2292번 벌집 (0) | 2022.03.18 |
| [백준 자바 JAVA] 1316번 그룹 단어 체커 (0) | 2022.03.17 |




댓글